Smith-diagrammet: Historien bak og hvorfor det er så viktig for RF-designere

Nybegynnere innen RF-konstruksjon som prøver å lage en direkte forbindelse mellom to komponenter – for eksempel fra en spenningsstyrt oscillator (VCO) til en mikser – har utvilsomt lagt merke til merkelige, sirkulære grafer på komponentdatablader, slik som disse for Maxim Integrated MAX2472, en VCO-bufferforsterker på 500 til 2500 megahertz (MHz) (figur 1). Det er ikke tvil om at disse grafene, som kalles Smith-diagrammer, er svært forskjellige fra alt som observeres i algebra- eller statistikkundervisning.

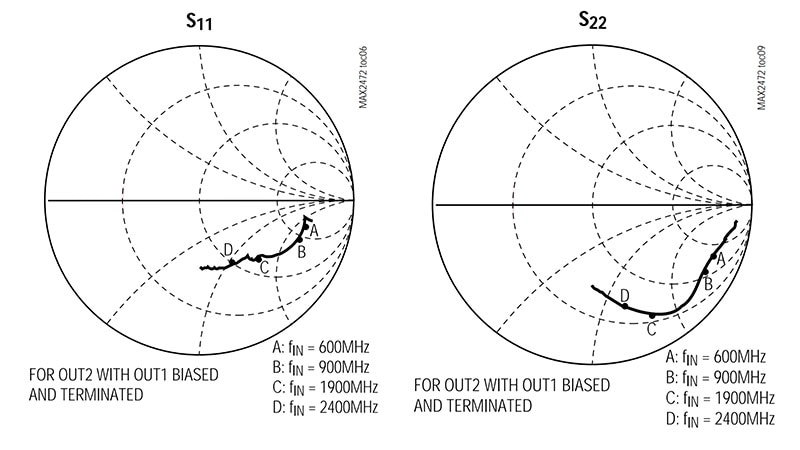Figur 1: Mange RF-komponentdatablader inkluderer Smith-diagrammer som viser verdiene til viktige parametere ved forskjellige driftsfrekvenser, for eksempel disse for Maxim MAX2472 VCO-bufferforsterkeren ved 600, 900, 1900 og 2400 MHz. (Bildekilde: Maxim Integrated)

Diagrammet er oppkalt etter Phillip Smith, en ingeniør ved Bell Telephone Laboratories, som utarbeidet og forbedret det mellom 1936 og 1939 mens han jobbet med å forstå overføringslinjer og stående bølger, som da ble ansett som «høye frekvenser» på opptil 1 MHz (kalt megasykluser per sekund på den tiden). Hans merkelige sirkulære diagram har blitt det mest nyttige og kraftige verktøyet når det kommer til å arbeide med og optimalisere høyfrekvente kretser med tanke på inngangs- og utgangsimpedans, selv i vår tidsalder med kraftige datamaskiner og verktøy for dataassistert utforming (CAD – computer-aided design).

Ett av de mange bruksområdene til Smith-diagrammet er å gi en effektiv måte å visualisere konstruksjonsalternativer på når mellomtilstandskilder og lastimpedanser skal samsvares, noe som er svært viktig i mange kretser, spesielt i RF-konstruksjoner. Det er to grunner til at slik samsvaring er svært viktig:

• For det første, for å realisere maksimal effektoverføring fra en kilde til en last, må kildens komplekse impedans R_S + jX_S være lik det komplekse konjugatet R_L - jX_L for lastimpedansen:

Der R er den resistive (virkelige) delen av impedansen, og X er den reaktive (induktive eller kapasitive) delen (figur 2).

Figur 2: En stor utfordring ved RF- og overføringslinjekonstruksjoner er å sørge for at kilden «ser» en lastimpedans, som er den komplekse konjugaten til kildens impedans, selv om lastimpedansen ikke er der. (Bildekilde: HandsOnRF.com)

• For det andre, selv om et slikt effekttap ikke er noe problem (det er nesten alltid et problem), er det nødvendig med impedanstilpasning for å minimere refleksjon av energi fra lasten tilbake til kilden, noe som kan skade kildens utgangskretser.

Smith-diagrammet viser følgende

Smith-diagrammet er et polart diagram av den komplekse refleksjonskoeffisienten (også kalt gamma og symbolisert med rho (Γ)). Det lykkes i å vise det som i starten kan synes å være en nesten umulig oppgave: Den simultane grafikken av de virkelige og imaginære delene av en kompleks impedans, der den virkelige delen R kan spenne fra 0 til uendelig (∞) og den imaginære delen X kan spenne fra minus uendelig til pluss uendelig – og den kan gjøre alt dette på et enkelt papirark.

Et forenklet Smith-diagram som viser sirkler med konstant motstand og buer med konstant reaktans, er et godt utgangspunkt for å forstå arrangementet (figur 3). En ekstra fordel er at diagrammet også gir en måte å vise spredningsparametere (S-parametere) på og hvordan verdiene til disse er relatert til faktiske maskinvaremålinger og betraktninger.

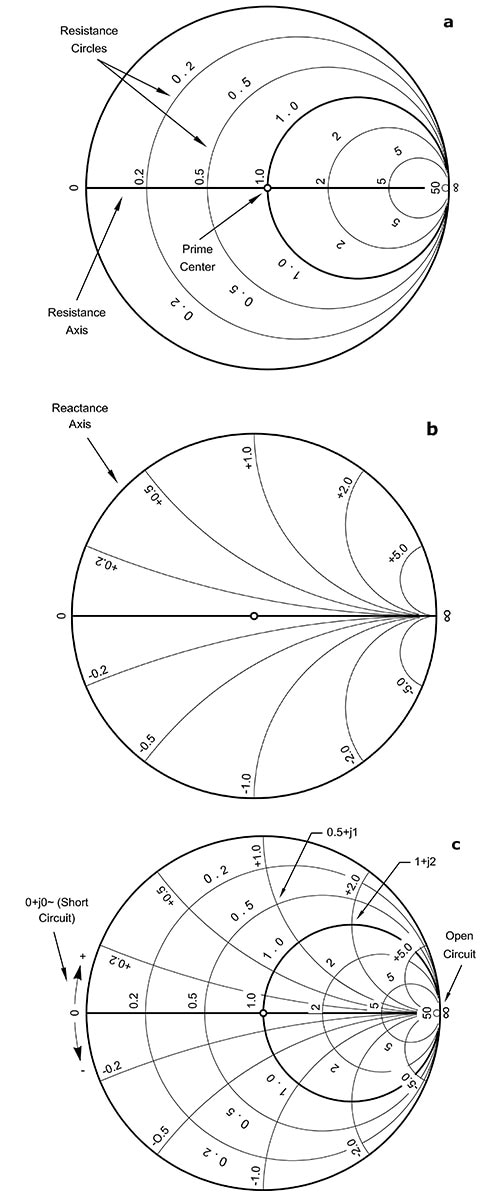Figur 3: Smith-diagrammet viser buer med konstant motstand (a) og sirkler med konstant reaktans (b) som er slått sammen og overlagt hverandre (c) for å gi et perspektiv på tvers av alle impedansmuligheter. (Bildekilde: ARRL.org)

Når disse komplekse impedansverdiene er merket på Smith-diagrammet, kan diagrammet brukes til å identifisere mange parametere som er avgjørende for å forstå situasjonen til RF-signalbanen eller overføringslinjen, inkludert:

• Komplekse refleksjonskoeffisienter for spenning og strøm.
• Komplekse overføringskoeffisienter for spenning og strøm.
• Effektrefleksjon og overføringskoeffisienter.
• Refleksjonstap.
• Returtap.
• Tapsfaktor for stående bølge.
• Maksimal og minimum spenning og strøm, samt stående bølge-forhold (SWR – standing wave ratio).
• Form, posisjon og fasedistribusjon kombinert med stående bølge, spenning og strøm.

Men dette er bare en del av Smith-diagrammet. Selv om det er nyttig og ofte nødvendig for designere å kjenne til de ovennevnte parametrene, kan Smith-diagrammet veilede analyser og konstruksjonsbeslutninger, inkludert:

• Visning av komplekse impedanser som funksjon av frekvens.
• Visning av S-parametere for et nettverk som funksjon av frekvens.
• Evaluering av inngangsreaktans eller susceptans for åpne og kortsluttede ledningsstumper.
• Evaluering av effekten til shunt- og serieimpedanser på impedansen til en overføringslinje.
• For å vise og evaluere egenskapene til inngangsimpedansen for resonante og ikke-resonante ledningsstumper, inkludert båndbredden og Q.
• Konstruksjon av impedanstilpassende nettverk som bruker én eller flere åpne eller kortsluttede ledningsstumper, kvartbølgelinjeseksjoner og konsentrerte L-C-komponenter.

Smith-diagrammets fordeler

Ved første øyekast kan det vanlige, fullstendig detaljerte Smith-diagrammet se ut som et nesten uforståelig sammensurium av linjer som går i alle retninger (figur 4), men det er egentlig bare en mer høyoppløselig, detaljert gjengivelse av det forenklede diagrammet som ble vist tidligere. Du kan laste ned en utskriftsvennlig versjon av et Smith-diagram fra ressursene i DigiKey sin innovasjonshåndbok (DigiKey Innovation Handbook) på nett.

Figur 4: Et typisk Smith-diagram kan se imponerende ut, men det er bare en mer høyoppløselig, detaljert gjengivelse av det forenklede diagrammet som ble vist tidligere. (Bildekilde: DigiKey)

Smith-diagrammet viser mer enn bare én enkelt løsning på mange konstruksjonsrelaterte problemer: Det viser mange av de mulige løsningene. Designere kan deretter fastsette hvilke som tilbyr et passende sett med komponentverdier for den bestemte situasjonen, for eksempel praktiske verdier for impedanstilpassende induktorer og kondensatorer. I de fleste tilfeller er diagrammets tallskalaer «normalisert» til systemer på 50 ohm (Ω), da dette er den vanligste impedansen som brukes i RF-konstruksjoner.

Smith-diagrammet er så viktig og nyttig at mange testinstrumenter for RF- og mikrobølgekonstruksjoner, for eksempel vektornettverksanalysatorer (VNA – vector network analyzers), kan kartlegge og vise det. For eksempel tilbyr Teledyne LeCroy T3VNA VNA en slik modus (figur 5).

Figur 5: T3VNA-vektornettverksanalysatoren kan vise innhentet data i Smith-diagramformatet. (Bildekilde: Teledyne LeCroy)

Hvor vanskelig er det å lære å bruke Smith-diagrammet? I likhet med de fleste andre slike spørsmål, er dette nesten det samme som å spørre forskjellige elever om hva de syns om vanskelighetene forbundet med matematisk analyse eller teorien om elektromagnetiske felt: Det kommer an på. Det finnes mange opplæringer i tekst- og videoformat på nett som begynner med det grunnleggende om Smith-diagrammer og deretter tilføyer ligninger for overføringslinjer og analytiske perspektiver. De går også gjennom en rekke eksempler på hvordan det brukes. Det finnes selvsagt også apper og programvare som gjør det enklere å lage grafiske fremstillinger, utarbeide problemet og evaluere alternativer ved å bruke Smith-diagrammet. Det hjelper imidlertid å først forstå diagrammets grunnprinsipper før du tyr til disse.

Konklusjon

Det er utrolig at et grafisk verktøy som ble utviklet for over 80 år siden, lenge før RF-konstruksjonene slik vi kjenner dem i dag, fremdeles er et av de viktigste ressursene for både papir- og programvarebaserte RF-konstruksjonsutfordringer. Smith-diagrammet brukes i begge disse tilfellene som et kraftig verktøy for å vise og vurdere RF-parametere og få innsikt i konstruksjonsalternativer og deres tilknyttede avveininger. Den beste måten å finne ut mer om kraften i Smith-diagrammet på, og hva det kan gjøre for deg, er å bruke det og arbeide gjennom noen av de mange publiserte eksemplene.

Anbefalt lesing

1 – «Smith-diagrammet: Et ‘eldgammelt’ grafisk verktøy som fortsatt er viktig innen RF-konstruksjon»

https://www.digikey.com/en/articles/the-smith-chart-an-ancient-graphical-tool-still-vital-in-rf-design

2 – «Saw-filtre redder trådløse produkter fra upraktiske frittstående implementasjoner»

https://www.digikey.com/en/articles/saw-filters-rescue-wireless-products-from-impractical-discrete-implementations

3 – «Forstå det grunnleggende om lave støynivåer og effektforsterkere i trådløse konstruksjoner»

https://www.digikey.com/en/articles/understanding-the-basics-of-low-noise-and-power-amplifiers-in-wireless-designs

4 – «Bruke logaritmiske forsterkere til å øke følsomhet og ytelse i RF-konstruksjoner med brede dynamiske områder og optiske forbindelser»

https://www.digikey.com/en/articles/use-log-amps-to-enhance-sensitivity-logarithmic-amplifiers